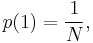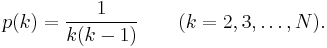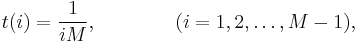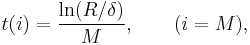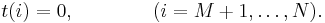Soliton distribution

A soliton distribution is a type of discrete probability distribution that arises in the theory of erasure correcting codes. A paper by Luby[1] introduced two forms of such distributions, the ideal soliton distribution and the robust soliton distribution.

Contents

Ideal distribution

The ideal soliton distribution is a probability distribution on the integers from 1 to N, where N is the single parameter of the distribution. The probability mass function is given by[2]

p(1)= \frac{1}{N},
p(k)= \frac{1}{k(k-1)} \qquad (k=2,3,\dots,N). \,

Robust distribution

The robust form of distribution is defined by adding an extra set of values to the elements of mass function of the ideal soliton distribution and then standardising so that the values add up to 1. The extra set of values, t, are defined in terms of an additional real-values parameter δ (which is interpreted as a failure probability) and an integer parameter M (M < N) . Define R as R=N/M. Then the values added to p(i), before the final standardisation, are[2]

t(i)= \frac{1}{iM}, \qquad \qquad (i=1,2,\dots,M-1), \,
t(i)= \frac{\ln(R/\delta)}{M}, \qquad (i=M), \,
t(i)= 0, \qquad \qquad (i=M%2B1,\dots,N). \,

While the ideal soliton distribution has a mode (or spike) at 1, the effect of the extra component in the robust distribution is to add an additional spike at the value M.

See also

References

  1. ^ Luby, M. (2002), "LT Codes", The 43rd Annual IEEE Symposium on Foundations of Computer Science
  2. ^ a b Tuomas Tirronen (2005) "Optimal Degree Distributions for LT Codes in Small Cases", Helsinki University of Technology.